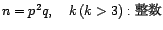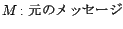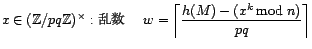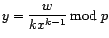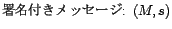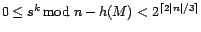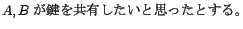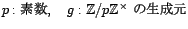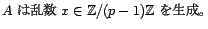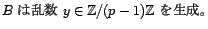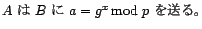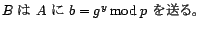[ホーム]->
[GnuPG]->
[algorithm]
[Next][Previous]
アルゴリズム
[(画像パッチなしの) w3m/emacs-w3m や lynx, Emacs-W3 などで見ている方へ]
以下、Z は有理整数環を表すことにします。また、x^y は、y が x の右肩に乗っていることを表します。
RSA 暗号
鍵生成
 [1]
[1]
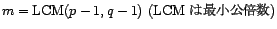


暗号化
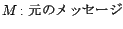
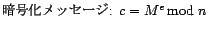
復号化
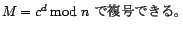
RSA 署名
鍵生成
 [1]
[1]
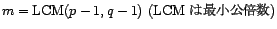


署名生成
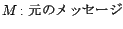
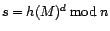
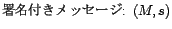
検証
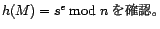
ElGamal 暗号
鍵生成
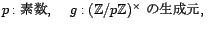



暗号化
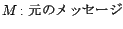
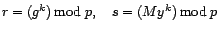
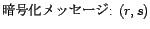
復号化
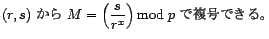
鍵生成
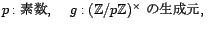

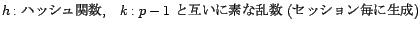

署名生成
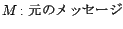
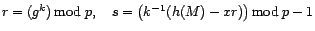
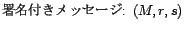
検証
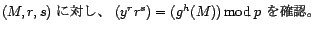
ElGamal 署名の変形で、安全性を保ったまま署名長を短くしたものです。
鍵生成

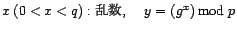
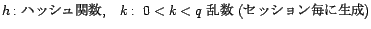

署名生成
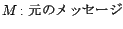
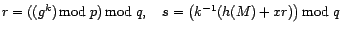
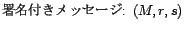
検証
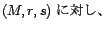
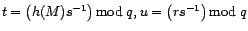
として、
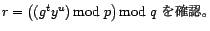
[註] 実際には、L を 64 の倍数でかつ 512≦L≦1024 なるもの、
また、p, q は 2^(L-1) < p < 2^L, 2^159 < q < 2^160 となるように取ります。
RSA と同じく素因数分解問題に基づきますが、RSA 署名に比較して署名の作成が数十倍高速です。
[w3m や lynx や Emacs-W3 で見ている方へ]
以下、【x】は x 以上の最小の整数を表すことにします。(ガウス記号ではなく ceiling の方。)
鍵生成
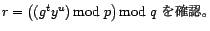 [1]
[1]

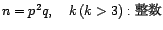

署名生成

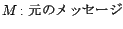
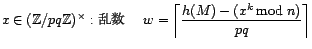
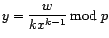
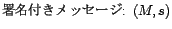
検証
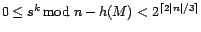
第三者に盗聴される可能性のある経路を使って秘密鍵を共有するためのアルゴリ
ズムです。安全性は離散対数問題に基づきます。
準備
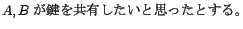
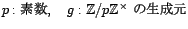
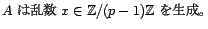
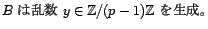
鍵配送
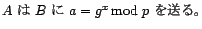
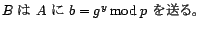
共有鍵の生成
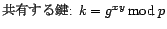
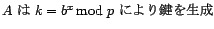
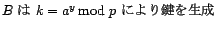
[1]
|p|, |q| がほぼ同じといっても、p,q が近すぎてもまずい。
これはフェルマーの因数分解法というもので簡単に因数分解できてしまうからである。
具体的には、p,q が近い場合、n=t^2-s^2 となるような t,s の組は t > √n となる t で t^2-n が平方数になるものとしてすぐに見つかる。(∵ n=((p+q)/2)^2-((p-q)/2)^2 と書けるから) すると、n=(t+s)(t-s) で分解できる。
[ホーム]->
[GnuPG]->
[algorithm]
[Next][Previous]
 [1]
[1]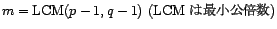


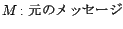
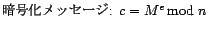
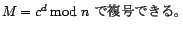
 [1]
[1]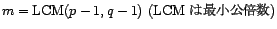


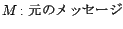
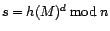
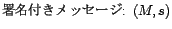
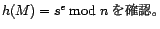
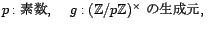



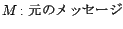
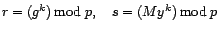
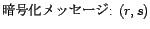
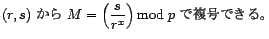
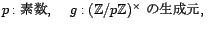

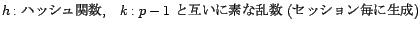

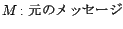
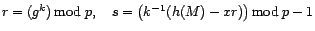
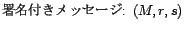
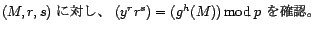

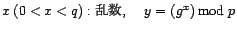
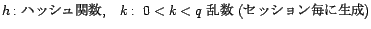

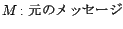
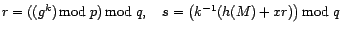
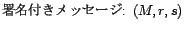
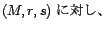
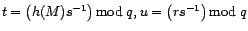
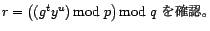
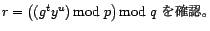 [1]
[1]