総務省『家計調査』 貯蓄・負債編 (平成18)年度より
|
。
|
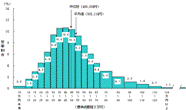
現金実収入階級別世帯分布（勤労者世帯）勤労者世帯について現金実収入階級別（標準級間隔5万円）の世帯分布をみると，平均値（502,114円）を下回る世帯が約6割（57.5％）を占めている |
(時事通信） - 12月8日 こ
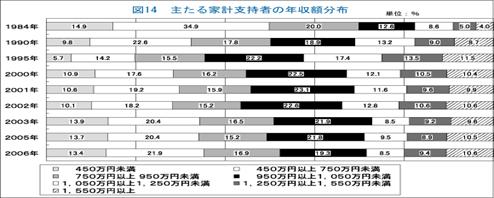
れまで平均値を取って「１０００万円以上」といわれてきた保護者の年収が、年収別の分布で詳細に見ると、１０５０万円未満の層が７割程度（０３年は
７２．７％）だったことも判明。４５０万円未満の層も０３年で１３．９％で、池田教授は「東大生の親に高額所得者が多いというのは間違い」とした。
標準偏差(Standard
Deviation, SD) ・パーセンタイルの使い方
例2：妊娠育児大百科
(生後10ヶ月)身長・体重のめやす
男の子は身長が68.4〜77.8cm、体重は7.6〜11.0kgぐらいに。女の子は身長が67.4〜75.8cm、体重は7.0〜10.2kgぐらいになってきます。（数字は3％タイル値から97％タイル値で表示）
http://www.sodatsu.com/data/ency/0_year/baby/baby10.htmlより
例3：某ミルクメーカーのサイト
例3
the group recommends that
SGA 1(small-for-gestational-age) be defined as a weight or length -2 SDs or less from the mean, and further subclassified
for weight, length, or both. The
Journal of Clinical Endocrinology and Metabolism.( Rapid
Electronic Publications issue),January 2, 2006
分散はばらつきの大きさの尺度である。「中心からの距離の２乗」の平均的な値と考えられる。したがって、その平方根である標準偏差は、おおよそ、「中心からの平均距離」と考えてよい。（厳密ではないが）
もしくは
問：なぜNで割るのではなく，N-1でわるのですか。答：分散を求めるときにn-1で割るのはｎで割ったのでは「本当の値」より小さくなりすぎる傾向があるから。たとえば、｛-1,1｝という値がそれぞれ０．５の確率で出る現象において、中心０からの平均距離は１である。
N=2の標本からこの分布の中心からの平均距離を推定する問題を考える。(1,1),(-1,1),(1,-1),(-1,-1)は1/4の確率で出現する、それに対応する
の値は、0, 2,2,0 なので
の値はそれぞれ0,1,1,0となり、その期待値は0.
5である。これは、本当の値１よりも小さすぎる。
の値はそれぞれ、0, 2, 2, 0である。いずれも確率1/4で出現するので、の期待値は真の値１に一致し、偏りがない。そこでは不偏分散と呼ばれる。Nが大きいときには，Nで割るかN-1で割るかでほとんど差はない。
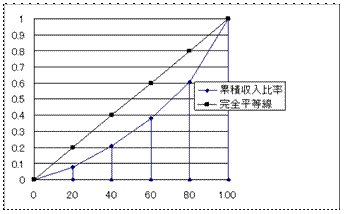
ローレンツ曲線
：データ(所得、資産など)：x1<...<xn, 累積和：Si=x1+...+xi,
(i=1,...,n) として
縦軸に累積和Si、横軸にi/n（下から何パーセントのところに位置するか）をとったグラフ
■ジニ係数:ローレンツ曲線と均等分布線の間の部分の面積比(0と1の間の値をとる)
これがおおきいほど不平等度が高い。０のときは完全な平等。
⇒不平等の尺度としてよく使われる。変動係数との違い:総和に意味がある場合にｼﾞﾆ係数。
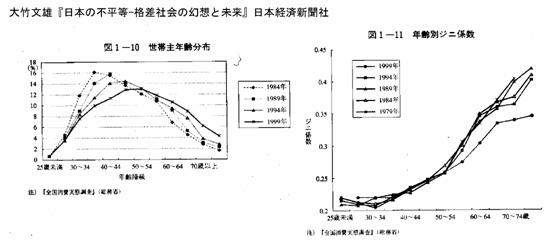
大竹文雄『日本の不平等-格差社会の幻想と未来』日本経済新聞社
ジニ係数による格差の計測にあたっての注意：高齢化は見かけ上の不平等を大きくする。単身家計の増加は低所得家計を増やし，見かけ上の平等をおおきくする。調査によって，所得の定義が異なる基礎データ（貯蓄動向調査,1989):
|
階級％ |
0-20 |
20-40 |
40-60 |
60-80 |
80-100 |
|
各五分位階級平均（万円） |
252.0 |
415.5 |
553.3 |
732.1 |
1253.4 |
4計算過程 (住人が5人と考えよう)
ステップ１：累積収入を求め、全収入との比率を計算。
|
累積相対度数 |
20 |
40 |
60 |
80 |
100 |
|
累積収入 |
252.0 |
667.5 |
1220.8 |
1952.9 |
3206.3 |
|
累積収入比率 |
0.079 |
0.208 |
0.381 |
0.609 |
1 |
注意：累積収入は
667.5=252.0+415.5、
1220.8=252.0+415.5+553.3
1952.9=252.0+415.5+553.3
累積収入の全収入との比率は0.079=252.0÷3206.3 0.208=667.5÷3206.3 ..のように計算
ステップ２：横軸に世帯の累積相対度数、縦軸に累積収入の全収入との比率をとり、方眼紙上にプロットしてローレンツ曲線（太い実線）を描くと下の図。EXCELで書くときは行と列を反対にして下の形にして散布図を書くとよい。
|
世帯の累積相対度数 |
累積収入比率 |
完全平等線 |
|
0 |
0 |
0 |
|
20 |
0.079 |
0.2 |
|
40 |
0.208 |
0.4 |
|
60 |
0.381 |
0.6 |
|
80 |
0.609 |
0.8 |
|
100 |
1 |
1 |
ステップ３：ローレンツ曲線よりも右の部分の面積は、台形公式を用いると、
(0 + 0.079)×0.2÷2
+(0.079+ 0.208)×0.2÷2
+(0.208 +0.381)×0.2 ÷2
+(0.381 + 0.609)×0.2÷2
+(0.609+ 1.00)×0.2 ÷2
= 0.079×0.2 + 0.208×0.2 + 0.381×0.2 + 0.609×0.2 + 1.00×0.1 = 0.3554
等分配線（点線）のつくる三角形の面積0.500から0.3554(ローレンツ曲線よりも右の部分の面積)を引くと、ローレンツ曲線と等分配線の間の面積0.1446がでる
その三角形の面積(0.5)との比を求めると、1989年のジニ係数0.289が求められる。
