http://mcobaya.hp.infoseek.co.jp/kisotokei/index.htm 講義のsite
![]() レポートなど送付先
レポートなど送付先
第2章
相関係数,単回帰分析
![]()
分散はばらつきの大きさの尺度である。「中心からの距離の2乗」の平均的な値と考えられる。したがって、その平方根である標準偏差は、おおよそ、「中心からの平均距離」と考えてよい。(厳密ではないが)
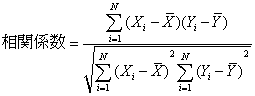
相関係数は何をはかっているのか。
第1象限ではX、Yとも平均m(X),m(Y)以上なので、積(X-m(X)(Y-
m(Y))はプラスの値。
第2象限ではXは平均以上、Yは平均以下なので、積(X-m(X)(Y-
m(Y))はマイナスの値。
第3象限ではX、Yとも平均以下なので、積(X-m(X)(Y-
m(Y))はプラスの値です。
第4象限ではXは平均以下、Yは平均以上なので、積(X-m(X)(Y-
m(Y))はマイナスの値。
したがって、散布図が右上がりならデータの多くは第1象限と第3象限に集まり、(X-m(X)(Y- m(Y))の値はほとんどプラスになり、相関係数の分子もプラスの値になる。逆に
散布図が右下がりならデータの多くは第2象限と第4象限に集まり、(X-m(X)(Y- m(Y))の値はほとんどマイナスになり、相関係数の分子もマイナスの値になる。分母は相関係数の絶対値が1以下になるようにするための調整項。相関係数の絶対値が1であるとは完全な直線的関係。
X-m(X)<0,
Y-m(Y)>0 (X-m(X))×(Y-m(Y))<0 X-m(X)>0,
Y-m(Y)>0 (X-m(X))×(Y-m(Y))>0 X-m(X)>0,
Y-m(Y)<0 (X-m(X))×(Y-m(Y))<0
X-m(X)<0,
Y-m(Y)<0 (X-m(X))×(Y-m(Y))>0
|
|
||
|
|
|
|
|
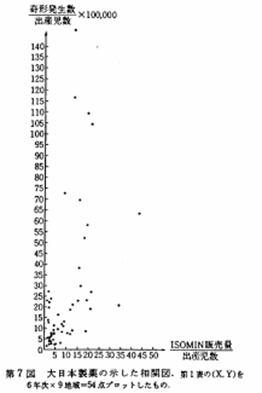
吉村功「アザラシ状奇形の原因1―サリドマイド仮説の成立に関する統計学上の争点について」『科学』岩波書店、1971年 データはyoshimura1.pdf(練習問題:妊婦のサリドマイド服用率の推定値Xと奇形発生率Yの相関係数を計算して、有意かどうか点検しよう。)
サリドマイドによる奇形説に反対する学者は縦軸に「奇形児数÷出生児数」、横軸に「サリドマイド販売量」をとって散布図(左図)を描き、両者に相関が認められないと主張。どこがおかしいか。相関係数=0.558, N=54」
第4図:人的資本と地方の労働生産性
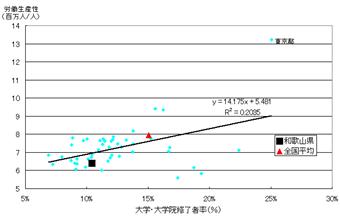
備考)総務省「事業所・企業統計調査」(平成13年)により作成。
『この第4図から、和歌山県は大学・大学院修了者の割合が少ないことが、労働生産性に影響しているのではないかと思われます。白書では、このように、地域の生産性は、より生産性の高い産業に特化している度合いが大きいほど、人的資本が高いほど、それに比例して高いということがいえるとしています。』 使うデータkogakurekis.xls (用いたデータが異なるので結果がやや異なる。)
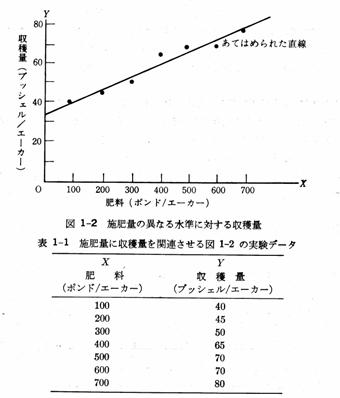
最小自乗法
回帰分析:相関はXとYの関連を図っている。XがYへの因果を前提として、Xが制御できる(わかる)とき、Yを予測しよう。
最小自乗法とは「当てはまり」の尺度として残差y(1)-
a - b*X(1)、y(n) - a - b*X(n)の平方和、すなわち残差平方和を
[y(1)- a - b*X(1)]2+...+[y(n) - a - b*X(n)]2
を最小にする。ただし、nは観測期間の長さ。myはyの平均
決定係数=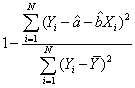
問:なぜ残差を自乗するのか。答え:自乗するとつねに正か0の値になり、残差平方和が0ならば当てはまりは完全になり、残差平方和が大きければ当てはまりが悪いと判断できる。
問:自乗しなくても絶対値でよいではないか。答:数学的に取り扱いがやっかい(性質がわかりにくい、計算機は絶対値の計算が苦手)
実際にはa,bを試行錯誤により決定すると言うことはなく、公式を使って、a,bを求める。
問:決定係数の小さな回帰分析場合、説明変数は無効か 答:小さな決定係数は雑音が大きいことをいっているだけで、説明変数の影響の有無とは関係ない。
問:XとYに相関があることはXとYに因果関係を意味するか。
問:XとYに相関がないことはXとYに関係がまったくないことを意味するか。
問:目で見たところ関連がなさそうなのだが、相関はないといってよいのか。
公式の導出
a,bは残差平方和最小化の一階の条件、すなわちa,bについて残差平方和を変微分したものがそれぞれ0であること。(aについて偏微分するとは、bは定数と見なし、aだけについて微分すること。同様にbについて偏微分するとはaは定数と見なし、bだけについて微分すること)
残差平方和をaで偏微分すると
(-1)[y(1) - a - b*x(1)]+...+( -1)[y(n) - a - b*x(n)].
これが0に等しいという条件はmy=a+b*mx (myとmx)はxとyの平均。)
残差平方和をbで偏微分すると
(-x(1))[y(1) - a - b*x(1)]+...+( -x(n))[y(n) - a - b*x(n)].
この二つの条件から
b=åt-1n(y(t) -my) (x(t) -mx)/å t-1n
(x(t) -mx)2
この公式はわかりにくいのですが、(3.5)にあるように、
XとYの共分散÷Xの分散
と考えるとすっきり。推定値aはmy=a+b*mxから得る。
|
|
|
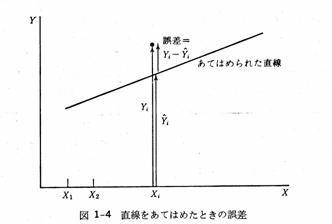
問:垂直距離を誤差と考えるのか。答:予測の誤差をできるだけ小さくしたい。
直線の傾き自体に興味があるときもある
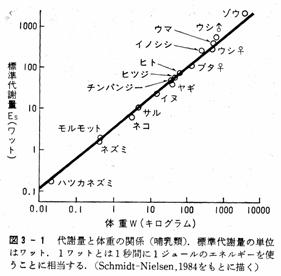
(本川達雄『ゾウの時間ネズミの時間』中公新書)
ogEnergy=log4.1+0.751*logWeight これを書き換えるとEnergy=4.1*Weight0.751
表面積(熱の発散)は体長の2乗、体重は3乗で増えるので、体重あたりのenergy発生率は体重の0.66乗のはずだが、実際に推定してみると0.75乗になっている。