分散の関数VARは、平均からの差の自乗をn-1で割ったものであることを既に紹介しました。これを「不偏分散」とも呼びます。２つの不偏の比を、「不偏分散比F」と呼び、その確率分布を利用して平均値の差の検定をおこないます。

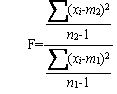課題９．前回の実験データを使って、各サンプルの不偏分散を算出し、その比を計算し、その分布をグラフ化してみよう。

（F確率分布）

　F確率分布は、正規確率分布やｔ分布のように左右対称の分布は取りません。分子に分母より大きい値が来る場合と、小さいものが来る場合が半々の確率で起きるはずなので、１を中心にほぼ半々の出現確率になります。さらに、分子のサンプル数、分母のサンプル数の違いによっても分布の形が異なります。下図は分子の自由度が１０、分母の自由度が１〜∞のF確率分布です。（注：F確率分布には２つの自由度があります。分子の分散の自由度、分母の分散の自由度です。）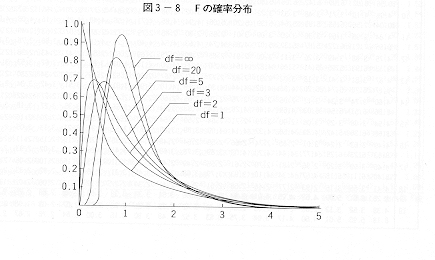

F分布を利用した検定（分散分析）

（例題）ある教科に関する教授法が改訂され、新しく２種類の教授法Ａ，Bが開発された。従来の教授法Ｃを含め３つの教授方の効果を確認するため、それぞれの教授条件にランダムに５人割り当て結果を測定したところ、以下のデータが得られた。


　このA条件6.6、B条件5.4、C条件３という平均値の違いは統計的に有意味な差と言って良いだろうか？

　分散分析では、得られたデータのバラツキのには、要因の効果（今回は教授法の違い）によって生じるバラツキとその他諸々の効果によって生じるバラツキが加算的に混ざり合ったものである、という考えから出発します。

　例題の場合、総平均は５なのでここのデータから５を引いたものが全体のバラツキです。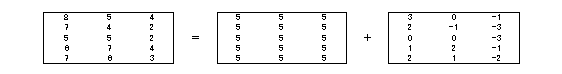

　教授要因の効果はそれぞれの条件の平均値に代表されている（母平均の推定値としてサンプル平均が使いますので）と考えて、教授要因の効果のバラツキは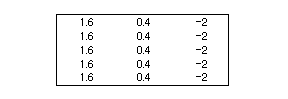

と考えます。実際のデータは一人ずつ異なる測定値になっていますが、それは教授法要因以外の要因の影響のために違うのであって要因の効果はみんな同じと考えます。したがって、その他の要因の効果（残差）は、全体のバラツキから教授要因の効果のバラツキ引いたものになります。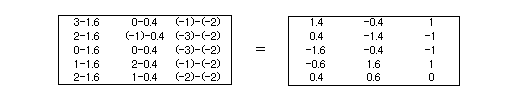

以上の操作で、次のように全体のバラツキが分解されました。

　次に、要因の効果のバラツキと残差のバラツキの比（F）を計算し、その値が同一母集団の分散比としては滅多に起きないズレ方であれば、帰無仮説（差がない）を捨て去り、「要因の効果は有意である」という結論を導きます。
　これが「分散分析」の原理です。

課題１０．エクセル上で実際にバラツキを分解しF値を計算してみましょう。

　　　要因の効果の自由度は３−１＝２
　　　残差の自由度は　　　　１５−２−１＝１２　です。

　　　　従って、要因の効果の不偏分散は　33.6／２＝16.8
　　　　　　　　　残差の不偏分散は　　　　　14.4／12＝1.2

　　　　　　　　　　　　　　F＝14.0　　自由度（2/12）

　　自由度（2/12）の１％水準のF値は6.93です。それより大きいF値がえられていますので、「１％水準で有意な差が見られる」と結論付けられます。


注）自由度に対応した棄却域のF値は、しばらく前までは「Fの表」から求めていましたが、現在は、統計プログラムでFの確率を直接求めることができます。