シュハートのノーマルチップの実験から、正規確率分布する母集団からｎ個のサンプルを取り出した場合、そのサンプル平均の分布は平均が母平均と一致し、標準偏差は母標準偏差σの√ｎ分の１になるという法則性があることが分かります（下図）。

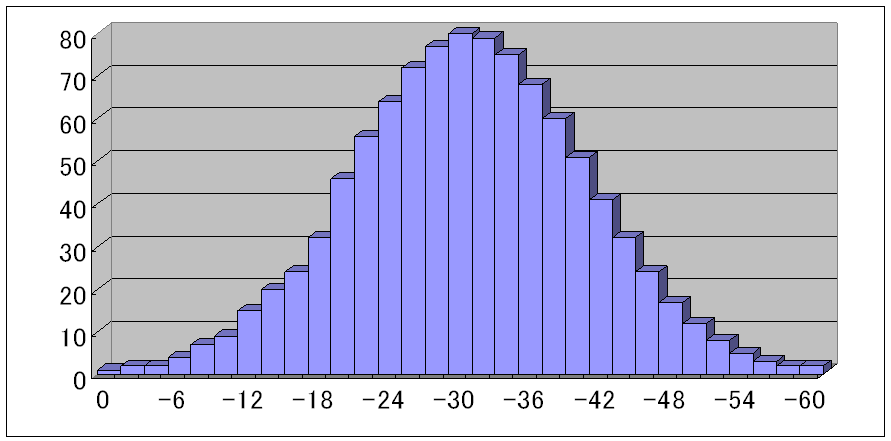
Figure２-2-1.シュハートのノーマルチップの分布（平均３０、標準偏差１０）

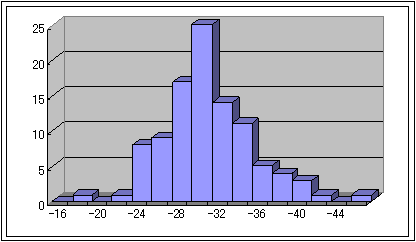
Figure2-2-2.５個のサンプル平均の分布（平均３０、標準偏差10/√5）

　今回のシミュレートでは、予め母平均とその標準偏差が分かっていましたが、普通は分かりません、そこでサンプル平均から母平均や標準偏差を推定せざるを得ません。また、平均値や標準偏差は測定対象によってまちまちな値を取ってしまうので、ｚ変換と同じように、平均０、標準偏差１になるように標準化し、その値をｔとします。標準化すればいろんな値を取るデータでも、サンプル数（自由度）が同じであれば一つの確率分布表で確率を読みとることが出来ます。

　　ここで　はサンプル平均、ｍは母平均の推定値、ｓは標本標準偏差を指す。


　このｔの確率分布は、左右対称で正規確率分布に近いのですが中央部が高くとがった分布をし、その尖り方（分布の仕方）はｎの数（自由度n-1）によって異なります。何故n-1が自由度として使われるのかと不思議に思うかもしれませんが、「母平均の推定に情報が１つ使われたしまったから」というのが一番簡単な説明です。

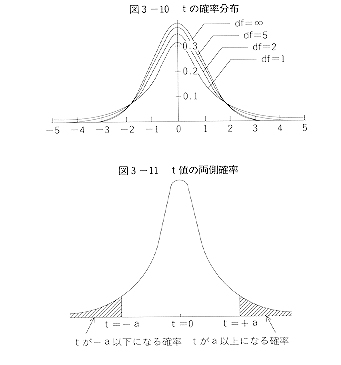
　統計の本にあるｔ確率分布表には、この両端が５％になるｔ値、１％になるｔ値が載っています。この両側の確率が平均値の差の検定に使われます。同じ母平均から取り出されたサンプルであれば、その平均値はこのｔ確率分布という規則性に従うはずです。

ｔ確率分布を使った２つの平均値の差の検定

　新しい教授法を開発し、これまでの教授法より優れていることを確認するため、ほぼ等しい力を持つ２つのクラスを対象に、一方に新しい教授法をふまえた授業を、もう一方に従来の教授法による授業を実施し、その効果を見るテストをおこない、以下のような結果が得られた。

表１．教授効果確認テストの結果

　得られた結果からすると、従来の教授法のクラスの成績は73.0、新しい教授法の方は78.7と新しい教授法が有効であるように見えます。しかし、これは単に偶然の差に過ぎないかもしれません。偶然の結果ではなく、新しい教授法が効果があると言ってよいかを確認するために統計的「検定」（ここではｔ検定）を使います。


（２つの平均値の差の検定の手順）

１．まず、２つの平均は差がない、つまり同じ平均をもつ母集団から取り出された２つのサンプル平均に過ぎないという前提（「帰無仮説」）から出発します。

２．もし、２つの平均値が同じ母集団から取り出されたサンプル平均にすぎないのであるならば、母平均ｍ（標準化すれば０）、標準偏差σ／√ｎの分布規則に当てはまることになります。

３．そこで、２つのサンプル平均のズレを示すｔ値を、下の公式を使って計算します。
　　
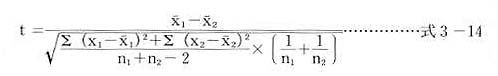
４．上の計算で得られたｔ値が自由度ｎ_１＋ｎ_２−２のときに起きうる確率（図3-11．の両端の確率）を求めます。（自由度が２引かれるのは母分散の推定に二つのサンブル平均が使われていることが上の公式から読みとれると思います）。

５．もし、ｔ値の確率が５％以下である場合、同じ母平均だとしたら１００回のうち５回しか起こらないズレが起きている。ということは、この２つは同じ母平均から取り出されたサンプルとは言えないのでは、ということで「帰無仮説」を棄却します。

６．「同じ」という「帰無仮説」を捨て去るのですから、２つの平均に統計的に差があると言える。という結論が導かれます。


注）１００回のうち５回起こると言うことは、本当に滅多に起きないことと言っていいのでしょうか？考え方によっては１００回のうち５回も起きるのです。薬の効果の検証や乗り物の安全性を問題にする場合はこのような基準は甘すぎるでしょう。しかし、心理学研究や社会学研究では５％水準がぎりぎりの基準として採用されています。
　また、滅多に起こらないからと帰無仮説を棄却しても５％水準の場合、１００の内５回は起きうるので、実際は差がなかったのにあるといってしまう危険性があります。これを「第一種の過誤」といい、逆に、差があるのに差がないという結論を出してしまう過ちを「第二種の過誤」と呼びます。そこで、帰無仮説を棄却する水準を「危険率」とも言います。


課題８．「分析ツール」を使って平均値の差の検定をしてみましょう。
　　　　
　　　　・「分析ツール」では「ｔ検定：等分散を仮定した２標本による検定」を使いましょう。
　　　　・結果には「両側確率」「片側確率」という２つの確率が出力されています。この確率が５％以下なら帰無仮説を棄却できます。
　　　　　　　ズレる方向が１方向だけ問題にするときは片側、どちらにズレるか分からないときは両側を使って検定します。
　　　　　　　今回は、新しい教授法が優れているという方向を問題にしますので、「片側検定」で良いでしょう。