![]()
推計学では、我々が処理するデータはある母集団から取り出されたサンブルデータだと考えて解析、処理を進めます。さらに、間隔尺度データや比率尺度データの母集団の多くは左右対称で一定の確率で分布(正規確率分布)すると考えます。
(正規確率分布)
平均値や標準偏差は対象によってまちまちな値をとりますが、平均との差を標準偏差で割るという「標準化(Z変換)」をすることで全てが同じ分布に表現できます(下図参照)。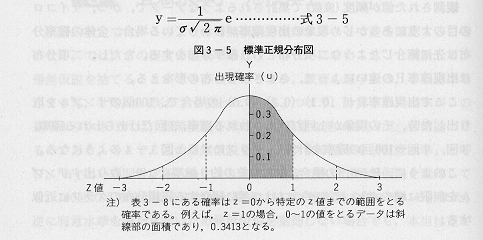
全ての値から平均値を引くということは全体の平均が0となります。
また、標準偏差で割るということは分散、標準偏差が1となります。上図の横軸の1,2,・・・は標準偏差(標準化されれば1)を単位にしたものです。統計の本には通常「z表」が載っており、そこにはzの値に対応した片側確率(0から右の確率)が示されています。エクセルでは「NORMSDIST」関数で直接求められますが、これで出力される確率は−∞〜z間での確率なので注意して下さい。
(シュハートのノーマルチップス実験)
998枚のチップに平均30、標準偏差10になるように0から60の値を書き込みます(下表参照)。すなわち、平均30、分散10の正規確率母集団を近似的に作ります。これらのチップをビニール袋に入れ、良くかき回して一枚のチップを取り出します。同じ操作を5回繰り返し、取り出されたチップの値をエクセルに記録します。これで、母集団から5つのサンプルを取り出すという作業のシミュレートが出来ました。サンプル平均を計算しましょう。
このシミュレートを70回(できたら100回)繰り返します。
| 値 | 枚数 | 値 | 枚数 | 値 | 枚数 | ||
| 0 | 1 | ||||||
| 1 | 1 | 21 | 27 | 41 | 22 | ||
| 2 | 1 | 22 | 29 | 42 | 19 | ||
| 3 | 1 | 23 | 31 | 43 | 17 | ||
| 4 | 1 | 24 | 33 | 44 | 15 | ||
| 5 | 2 | 25 | 35 | 45 | 13 | ||
| 6 | 2 | 26 | 37 | 46 | 11 | ||
| 7 | 3 | 27 | 38 | 47 | 9 | ||
| 8 | 4 | 28 | 39 | 48 | 8 | ||
| 9 | 4 | 29 | 40 | 49 | 7 | ||
| 10 | 5 | 30 | 40 | 50 | 5 | ||
| 11 | 7 | 31 | 40 | 51 | 4 | ||
| 12 | 8 | 32 | 39 | 52 | 4 | ||
| 13 | 9 | 33 | 38 | 53 | 3 | ||
| 14 | 11 | 34 | 37 | 54 | 2 | ||
| 15 | 13 | 35 | 35 | 55 | 2 | ||
| 16 | 15 | 36 | 33 | 56 | 1 | ||
| 17 | 17 | 37 | 31 | 57 | 1 | ||
| 18 | 19 | 38 | 29 | 58 | 1 | ||
| 19 | 22 | 39 | 27 | 59 | 1 | ||
| 20 | 24 | 40 | 24 | 60 | 1 |
以上の実験で平均30、分散10の正規母集団から70個のサンプル平均がどう分布するかがシミュレートできます。
課題7.ノーマルチップの実験を2人一組で行いその結果をエクセルにまとめ(サンプル平均の分布を集計し)て提出する。