（４）間隔、比率データの基礎集計（「階級別度数集計」の処理）


　名義尺度や順序尺度はそれぞれの値がとびとびの離散量です。従って、それぞれの値ごとの度数集計が簡単にできますが、間隔尺度以上のデータは値と値の間の距離も意味のある連続量で、値の範囲も広がりを持ちまちまちです。度数分布の集計を行うには、一定の範囲（階級）を指定しその範囲にあるデータの個数を集計します。これを「階級別度数集計」または「スストグラム」といいます。


課題５．先週の例題（例題４−１）のデータを度数集計して、分布をグラフ化しよう。


（度数集計の仕方）
１．集計の仕方は度数集計と同じく「区間配列」を用意して、それを基準に度数集計（Frequency）させます。問題は、区間配列ををどうするかです。平均値や最小値、最大値を参考に幅を決めます。

２．ここでは４３０万円が最小値で、４６２０万が最大値です。４００万から４６２０万までを１００万刻みで集計してみましょう。

３．刻み幅は間隔尺度ですのでとりあえず１００刻みに集計しますが、２０００万を超えると１００刻みでは０のクラスが多くなります。そこで、報告書にまとめる場合には２０００万以上として合わせてしまうか、１０００刻みに途中で変更したりしましょう。ただし、分布を考えるときには刻み幅を等間隔なものとして考えなければなりません。

（グラフ化の仕方）
１．グラフ化がしやすいように、ラベル類を付けた表を作成し直す。

２．作成した表を指定し、グラフ化をする（今回は、分布を確認するためのグラフなので収入を横軸にした縦棒グラフがよいでしょう）。

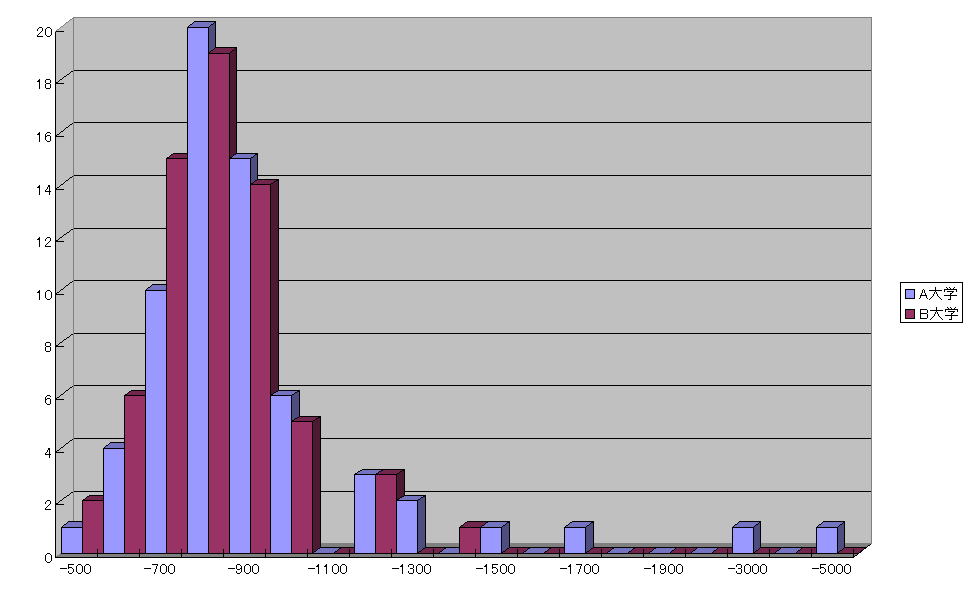
（グラフの解説）
　２群のデータの分布をグラフから見ると、最頻値は同じなのですがA大学の分布は右（大きい）の方に裾野が延びています。この３人ほどの値で平均が高いほうに引っ張られていることがわかります。

課題６．「分析ツール」にある「基本統計量」を使って各統計量を計算しよう。


　エクセルでは基本的な検定を中心とした統計処理が「分析ツール」として用意されています。「基本統計量」を使うと先週計算した統計量がまとめて出力されます。
　ここで出力されている分散や標準偏差はn-1で割った値です。なぜこれが使われるかは後で勉強してもらう課題ですが、n-1で割った方が「母分散」や「母標準偏差」に近い値が得られるからです（推計学では我々が手にしたデータは実際に存在する母集団から取り出された１つのサンプルデータであると考えます）。


（今まで出てこなかった統計量の解説）

標準誤差：標準偏差をサンプル数のルートで割った値。
　　　　　　　サンプル標準偏差は母標準偏差をルートｎで割った値となるというルールから算出される。

信頼区間：母平均が実際にある範囲を示す値で、通常、９５％の確率で存在する範囲を使います。
　　　　　　　　　標準誤差に自由度６４の0.25％のｔ確率分布のｔ値（1.9977）をかけた値。
　　　　　　　　　　　　　　　　　　　　ｔ（0.05/2,64）＝1.9977


尖度：分布の尖り具合をあらわす統計量
　　　　　公式は省略します。尖度や歪度より度数分布を見ることが大切です。


歪度：分布の左右対称ではない偏り具合を表す統計量