m=
(4)間隔、比率データの基礎集計
間隔尺度データも比率尺度データも目盛り間の距離は等しいので、平均値(合計してサンプル数で割る)や個別データーがその平均値からどのような距離にあるか(偏差)など距離的な整理(処理)ができます。間隔尺度データは値の持つ絶対的な比例関係は分析できませんが、基礎集計の仕方はほぼ同じです。
(例題4−1)A,B2大学の学生について親の収入を調査したところ以下の結果が得られた。
(単位:万円)
| A大学生の親の年収 | B大学生の親の年収 |
| 840 | 760 |
| 1200 | 850 |
| 450 | 1200 |
| 560 | 660 |
| 3000 | 820 |
| 750 | 680 |
| 1430 | 930 |
| 800 | 760 |
| 860 | 890 |
| 960 | 450 |
| 1300 | 560 |
| 740 | 710 |
| 640 | 820 |
| 580 | 580 |
| 720 | 1110 |
| 810 | 660 |
| 770 | 820 |
| 760 | 730 |
| 850 | 710 |
| 1200 | 660 |
| 660 | 520 |
| 820 | 710 |
| 680 | 650 |
| 930 | 580 |
| 760 | 910 |
| 890 | 810 |
| 980 | 1200 |
| 690 | 720 |
| 720 | 840 |
| 820 | 710 |
| 770 | 640 |
| 760 | 680 |
| 850 | 580 |
| 1300 | 810 |
| 660 | 760 |
| 1620 | 920 |
| 680 | 840 |
| 930 | 660 |
| 760 | 1320 |
| 890 | 770 |
| 980 | 820 |
| 590 | 610 |
| 840 | 810 |
| 1200 | 740 |
| 750 | 910 |
| 660 | 660 |
| 840 | 720 |
| 780 | 810 |
| 720 | 640 |
| 880 | 910 |
| 760 | 760 |
| 4620 | 810 |
| 680 | 430 |
| 930 | 620 |
| 760 | 760 |
| 890 | 580 |
| 700 | 730 |
| 690 | 620 |
| 720 | 810 |
| 820 | 670 |
| 770 | 760 |
| 760 | 710 |
| 850 | 800 |
| 600 | 640 |
| 800 | 760 |
課題4.上のデータの基礎集計を行おう。
間隔尺度データの基礎集計には、代表値を求める、バラツキを計算する、度数分布を集計するなどの作業があります。
(1)代表値の計算
代表値とはそれぞれのデータ群を代表する値のことで、平均(mean)、最頻値(mode)、中央値(median)などがあります。平均値は、
| m= |
という式で求められます。
エクセルでは関数が用意されていますので、以下の手順で平均値や中央値、最頻値を計算させることが出来ます。
1.結果を出力したいセルを指定(クリック)
2.挿入メニューまたは関数アイコン関数をクリックして必要な関数(例えばmean)を選ぶ。
3.関数のダイアログに集計したいデータの範囲を指定して「OK」を押す。
という操作で簡単に代表値が計算されます。
注)平均といえば、通常は上式の「算術平均」を指しますが、比の平均である「調和平均」、幾何的な平均(積をルートで開平する)である「幾何平均」などもあります。
(2)バラツキ(散布度)の計算
バラツキとはデータの分布の仕方を表す値(指標)で、レンジ(range 最大値最小値の幅)、偏差平方和、(平均値と個々のデータの差を自乗したものの合計)、分散(偏差平方和をサンプル数Nで割ったもの)、標準偏差(分散をルートで開平したもの)などがあります。四分偏差(quartile
deviation)については後で説明します。
分散の公式
| |
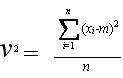 |
(ここでmは平均値)
(補足)
エクセルにはバラツキを集計する関数もそろっています。ただし、rangeは「最大値(MAX)」「最小値(MIN)」を計算させて求めます。
「VAR」は分散、「STDEV」は標準偏差です。ただし、「VAR」にも「STDEV」にもAやPが付いた関数があります。Pの付いたものは、分母がサンプル数nで割ったものであり、Aが付いた(付かないものも同じ)はn−1で割ったものが出力されます。n−1で割ると母集団の分散により近い値が得られということから通常、n−1で割ったものが「分散」「標準偏差」と呼ばれ、サンプル数で割ったものを「サンプル分散」「サンプル標準偏差」と区別して使い分ける場合があります。