「私の専門は数論です」というと「えっ 1 とか 2 とか 3 とかを研究しているの?」 と言われることが多いのですが、皆さんは数というと何を思い浮かべるでしょうか。 整数、有理数、それとも実数でしょうか。実数(Rと書きます)というのは有理数(Qと 書きます)の間を埋めて出来る数です。これは数直線の上で考えれば解りやすいかもし れません。
-1 0 2/5 1 √2 2 3
-----------|-----------|----+------|----+------|-----------|------
例えば整数の点は、数直線の上ではポツポツと間を置いて並んでいます。しかし 2/5 等も含めた有理数全体では、どんな異なる二点を取ってもその間に無数の有理点がある くらい詰まっています。しかし実はそれでも隙間だらけなのです。それを埋めてくれる のが √2 等の無理数で、これらを合わせて初めて実数全体が得られます。
ところで、「有理数の間の埋め方」(数学の世界では完備化と呼ばれます)は一通りでは ありません。実は各素数pに対して一つずつ、実数とはまた別の「間の埋め方」があり ます。そうやって得られた数はp進数と呼ばれます(Qp と書きます)。実数と違って、 p進数には順序というものはありません。従って数直線のようなものでイメージするこ とは出来ません。同様に正負という概念もありません。言ってみれば、年功序列も男女 差別もない世界と言えるでしょうか。このような世界が素数ごとに無数に広がっている のです。大抵の数には自分の得意な世界というものがあり、実数、或いはこのp進数の どこかの世界に活躍出来る場(一つとは限らない)が与えられています。数論では実数も p進数も対等に扱って初めて数の深い性質が分ることが多いです。平等博愛の精神が大 切という訳ですね。
. . R
. Q2
∧
Qp <Q> Q3
∨
Q11 Q5
Q7
私が興味を持っているのは、こういう世界の中での微分方程式の振舞いです。「こんな 変な世界で微分方程式なんかを考えて何の役に立つの? それに整数と微分方程式とど んな関係があるの?」とおっしゃる方、もっともです。実際、解析を専門にしている数 学者の友人からも同じことを言われてしまいました。しかし、数学の世界では「美しい 理論はいつか必ず役に立つ」という格言があります。この一見とんでもない世界が、実 は整数論で現われる面白い現象と極めて深く結びついていることに今でもよく驚かされ ます。
今研究している内容を一言で説明するのはとても無理なのですが、下にちょっとした イラストを描いてみました。
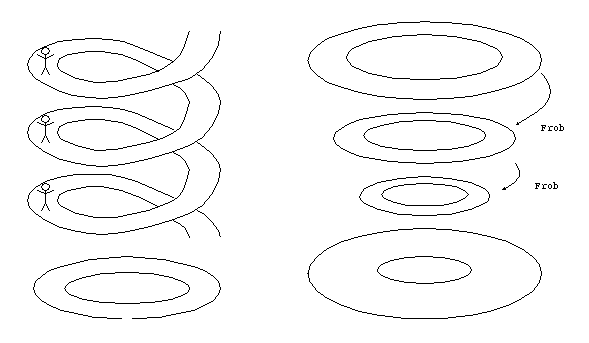
上の左の図は、普通の複素数の世界での微分方程式のモノドロミーというものに関する ものです。(複素数は実数を自然に拡張して得られる世界です。そのため昔から良く研 究されてきました。) 一方、右の図は、 p進数の世界での微分方程式のモノドロミー に関するものです。一般にp進数は図に表わすのが大変難しくこの図も無理している部 分が多いのですが、なんとなく似ていることはお解りになることと思います。この「似 ている所」をしっかり見ることで、普段は見えないp進数の世界を捉えて、今迄説明が つかなかった数の性質を調べられたらなあというのが現在の夢です。